Geometría para Primer Ciclo de Primaria - 1

Taller de MARTEMÁTICAS - 1  El punto y la recta

La base primigenia de la geometría es el punto; por sí solo no es nada, no es un objeto físico, pero sirve para formar todos los que sí lo son, todo lo que nos rodea. ¿Qué es una recta, sino una sucesión de puntos en la misma dirección? y ¿no es al mismo tiempo el punto una forma de representar la intersección entre dos rectas? Recta y punto son, pues, dos de los elementos principales de la geometría, junto con el plano, y son precisamente estos dos primeros elementos los que vamos a abordar en este capítulo.

Explicar estos conceptos a los niños de una manera clara mediante ejemplos, es el principal objetivo de este apartado, para ello, comenzaré mostrando ambos conceptos en la vida real, y haré lo propio en el Arte, destacando el papel protagonista de punto y recta en distintas obras artísticas. Tras esto, sin entrar en definiciones complejas, y con los conceptos de punto y recta claros gracias a los ejemplos, el objetivo es que empiecen a ver la geometría y sus elementos como algo familiar, como algo que tienen a su alcance para comprender el mundo que les rodea y como una herramienta tan maravillosa como necesaria para desarrollar su creatividad.

Pondré también un enlace con un vídeo para mostrar a maestros y a niños algunos pequeños consejos para trabajar mejor con líneas rectas, tanto a mano alzada como con elementos auxiliares cuando no tenemos una regla a mano, o simplemente no necesitamos una recta "perfecta". Por último, veremos una serie de posibles recursos y actividades enfocadas a desarrollar tanto las habilidades manuales y la creatividad, como el pensamiento matemático de los niños, sirviéndonos de juegos y de papel y lápices, así como de software informático accesible para todos, como el programa Paint de Windows, o la aplicación gratuita de código abierto Tux Paint.

El punto y la recta en nuestro entorno

Es importante que los niños sepan cómo utilizar e interpretar el punto. Lo suelen percibir como un "círculo pequeñito", pero cualquier objeto, circular o no, aunque sea tan grande como el sol, se puede representar por un punto si está lo suficientemente alejado. Algo similar ocurre con la línea del horizonte que, aunque es curva, y yo soy partidario de explicárselo así casi desde el principio (algo fácil de hacer con un globo terráqueo), tienen que comprender que un tramo muy pequeño de esa curva, como es la línea de horizonte para nosotros, en proporción con el tamaño de la tierra, lo vamos a percibir como una línea recta, y lo solemos representar así en nuestros dibujos cuando queremos pintar del horizonte.

Siguiendo el mismo razonamiento, una persona vista desde muy lejos, también se puede representar por un punto, de tal forma que el público de un estadio deportivo se percibiría por una aglomeración de puntos. Esto ofrece grandes posibilidades estéticas y creativas, como los mosaicos tan populares que se forman en los acontecimientos deportivos con la participación del público. Retomaremos posteriormente esta idea con ejemplos de obras de arte puntillistas o mosaicos romanos. Además de esto, si estamos utilizando una imagen de un campo deportivo para explicar esa interpretación del público como agrupaciones de puntos, resulta conveniente centrar también su atención en las líneas rectas que pueden ver en cualquier campo o pista deportiva. Tenemos que aprovechar los conocimientos previos, lo que ya saben los niños y con lo que se sienten familiarizados, y la mayor parte de ellos practican algún deporte o, en su defecto, conocen estas líneas de verlas día a día en las propias instalaciones del colegio. El concepto de línea como elemento delimitador, como elemento contenedor, no es algo desconocido para ellos.

Otro ejemplo de la presencia de líneas rectas en nuestro entorno cotidiano son unas vías de tren que se pierden en la lejanía. Los cables de la propia electrificación de la vía en esta misma imagen, o las líneas paralelas de carreteras y autovías serían también buenos ejemplos.

Centrándonos en el entorno del hogar, basta con entrar en la cocina o el cuarto de baño para encontrarnos con otro ejemplo que les resultará a los niños muy familiar, donde la relación entre punto y línea vuelve a quedar patente. ¿Quién no conoce las típicas cadenas de bolitas que unen un grifo con el tapón de su desagüe? Cada bolita de la cadena podría representar un punto, y si la tensamos, los niños pueden observar claramente cómo esa sucesión de puntos forma una línea recta, tal y como definimos al principio.

Y otro ejemplo, también cotidiano y familiar para los niños, donde líneas rectas y puntos vuelven a coincidir, lo pueden encontrar simplemente al abrir su mochila y coger uno de sus cuadernos o libretas de muelles. La secuencia de puntos alineados estaría en este caso representada por los taladros del cuaderno donde va alojado el muelle, y la retícula del papel, ya sea de cuadros o de líneas simples como el de esta imagen, también estaría formada por líneas.

El punto y la recta en el Arte

Sin duda alguna, uno de los pintores que mejor nos puede iluminar en esta tarea es Wassily Kandinski, no sólo por la utilización en muchas de sus obras del punto y la recta como elementos básicos, sino por su empleo del color, muy en consonancia con el gusto y creatividad de los niños. Kandinski fue un pintor ruso, precursor de la abstracción y teórico del arte, que plasmó gran parte de sus investigaciones pictóricas en el libro "Punto y línea sobre el plano". Sus obras se prestan a ejercicios de interpretación por parte de los niños, a que identifiquen elementos geométricos y, sobre todo, a que les sirvan de inspiración y referente para sus propias composiciones pictóricas o, por qué no, escritas.

El pintor español, Joan Miró, puede ser otro estupendo referente, por la sencillez de sus composiciones y porque también es un pintor que suele gustar a los niños. Aunque pasó por diferentes etapas, es uno de los máximos representantes del surrealismo, y se prodigó en el uso del punto y de la línea como elemento compositivo en muchas sus obras. 

Aunque volveremos inevitablemente a él, en el capítulo dedicado a cuadrados y rectángulos, Piet Mondrian es otro pintor, cuya obra nos puede resultar igualmente útil para mostrar a los alumnos hermosas composiciones hechas a base de rectas, como la de la imagen de la izquierda, correspondiente al cuadro: "Composición con rojo, amarillo y azul". Mondrian fue un pintor vanguardista holandés, fundador del neoplasticismo, que evolucionó desde el naturalismo y el simbolismo hasta la abstracción.

Anteriormente, veíamos un ejemplo de cómo el público de un estadio deportivo, se suele organizar para formar determinadas imágenes a modo de mosaicos humanos, donde cada pieza del mosaico, cada persona, sería uno de los puntos de la composición. Un punto de origen para ese tipo de representación visual, lo encontramos en los mosaicos romanos, como el de la imagen de la derecha. En este sentido, además de buscar imágenes sencillas como ésta, y teniendo en cuenta la edad de los niños de este ciclo, es conveniente proporcionarles rotuladores de punta muy gruesa, para que puedan experimentar más fácilmente, si tienen que reproducir o pintar sus propias composiciones de puntos. Lo veremos en el apartado de actividades.

Por último, para cerrar este apartado, nada mejor que mostrar a los niños un cuadro de Georges Pierre Seurat, pintor francés, fundador del Neoimpresionismo y creador del puntillismo. Esta técnica pictórica se basa en dibujar y pintar mediante puntos, con un uso muy reducido o nulo de líneas o manchas de color planas. Conviene mostrar a los niños, no sólo buenos ejemplos de obras de arte importantes realizadas con esta técnica, sino también algún detalle ampliado de las mismas para que visualicen cómo es el punto el elemento constructivo de la imagen.

Mejorar la precisión en el trazado de líneas rectas

Antes de nada, quiero hacer hincapié en que esto no tiene por qué ser una obsesión para nosotros, como maestros o padres. Los niños necesitan tener un amplio margen de libertad a la hora de representar la realidad, si no queremos perjudicar su creatividad, que es lo que solemos hacer los adultos aún sin proponerlo. Pero, dicho esto, llega un momento en que necesitan saber que, en ocasiones, será necesario y les será de gran utilidad mejorar sus destrezas en el dibujo, su precisión a la hora de trazar mejor una línea recta a mano alzada, sobre todo desde el punto de vista de las matemáticas y los conceptos geométricos que han de ir asimilando.

Existe la falsa creencia, a la que colaboran algunos maestros y muchos padres, de que hay niños completamente "negados" para dibujar, y en ocasiones esto desemboca en una resignación tan errónea como injusta. Cualquier niño, con la motivación apropiada, puede aprender algunas estrategias que le ayuden en el dibujo. Es cierto que no es una tarea fácil, pero siempre merece la pena intentarlo.

En el siguiente vídeo hablo de esto mismo y, de forma práctica, me centro en dos o tres consejos que pueden ayudar no sólo a enseñar a los niños a mejorar su precisión en el dibujo de líneas rectas, sino también a que lo hagan algunos adultos, de hecho el vídeo está destinado a padres y maestros, que serán los que transmitirán los distintos consejos a los niños cuando consideren oportuno. Un detalle que añado a lo comentado en el vídeo, es la importancia de explicar a los niños que hagan los trazos con suavidad, casi acariciando el papel. Al repasarlos posteriormente, ya podrán apretar más para mejorarlos.

Recursos y actividades de comprensión y representación de puntos y rectas

Las posibilidades con estos dos elementos básicos de la geometría son prácticamente infinitas. Muchas de ellas ya les son conocidas a niños y maestros, y las han utilizado desde Educación Infantil en sus juegos y para desarrollar las primeras destrezas en el dibujo y la pre-escritura. Se trata pues de retomarlas y encauzarlas de forma apropiada a nuestro objetivo. Vamos a ver algunos ejemplos:

1. Juego de mosaicos

Una buena forma de comenzar las actividades es mediante un juego de mosaicos, como los que tantas veces habrán utilizado en la etapa de Infantil. En las tiendas especializadas suele haber una gama muy amplia, aunque conviene empezar proporcionándoles algunos sencillos, por la claridad con la que pueden ver la relación entre línea y punto. Como haremos luego, con lápiz y papel, una buena actividad es que comiencen situando los vértices de rectángulos y otras figuras para, a continuación, formar líneas entre dichos vértices. Siempre, cuando observemos que han asimilado los conceptos de vértice (punto) y línea recta, es recomendable dejarles al menos unos minutos para que se expresen libremente con éste u otros materiales, trabajando con formas o cualquier otra cosa que se les ocurra.

2. Unir puntos con líneas

Tanto en esta etapa como en la anterior, los niños están también familiarizados con dibujos que se construyen a base de unir puntos, normalmente según una numeración. Volvemos pues a encauzar ese tipo de actividad hacia nuestro objetivo. La imagen de la izquierda es sólo un ejemplo de lo que podemos hacer en este sentido. Se trata de una hoja DIN-A4 en la que he dibujado una serie de cuadrados y rectángulos que han de servir de referencia. Junto a ellos, hay una serie de puntos, que no son otra cosa que los vértices reproducidos de las mismas figuras para que los niños los unan con el lápiz; siempre, empezando por los más pequeños. Los más grandes, tienen los vértices numerados para facilitar la tarea, y en la parte inferior hay un rectángulo apaisado que ha de servir también de referencia para trazar paralelas por los vértices indicados. Una actividad de este tipo ofrece muchas posibilidades, como la de introducir sutilmente el concepto de paralelismo, como se puede ver en el cuadrado superior derecho de la hoja.
Lo recomendable en esta actividad es que los niños puedan completarla libremente, repasando líneas con pinturas o rotuladores, coloreando figuras a su gusto, uniendo diagonales, etc.

3. Jugando a las tres en raya

Se trata de un sencillo juego, conocido por todos, que probablemente no necesite gran explicación. Los niños tienen que conseguir alinear tres fichas (puntos), colocándolas por turnos e intentando que no lo haga el otro jugador. Conociendo a nuestros alumnos, los podemos emparejar convenientemente para equilibrar los juegos. Este juego, no sólo ayuda a los niños a fijar los conceptos de punto y línea, sino que además es una excelente herramienta para trabajar diversas habilidades como la concentración, la memoria e incluso el ingenio.

4. Trabajar el punto y la línea con programas informáticos

Si los alumnos no conocen ya el programa Paint que viene incluido con Windows, es éste un buen momento para presentárselo. Es un programa tan sencillo como limitado, pero precisamente por eso, es ideal para introducir a los niños en el uso de programas de Diseño por Ordenador, y en el uso en sí de la propia informática. El programa es muy intuitivo, y se trata de momento de centrar la atención únicamente en unas pocas opciones. Por ejemplo, podríamos abrir el dibujo original que hemos usado en la actividad 2, y ponerles la misma tarea que tenían que hacer anteriormente, es decir, unir puntos mediante líneas rectas según las indicaciones dadas, sólo que en esta ocasión usarán un programa informático.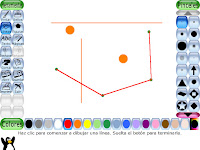

Otra muy buena opción para introducir a los niños en este tipo de aplicaciones es el programa gratuito de código abierto Tux Paint, que presenta una interface adaptada a los niños y que ofrece bastantes más posibilidades técnicas y creativas que Paint. Se puede decargar directamente desde la página oficial del programa: http://www.tuxpaint.org y su utilización también es muy sencilla y fácil de asimilar por los niños. En este caso, al igual que con el programa anterior, podemos empezar con una actividad de dibujo más dirigida, enfocada al trazado de líneas rectas a partir de puntos, para permitirles a continuación trabajar y experimentar libremente con el programa.

5. Jugando a las cuatro en raya

Se trata, de nuevo, de un juego muy popular y positivo para los niños, que tampoco requiere gran explicación, y donde también los elementos de punto y línea recta están claramente representados. Se podría jugar con un juego físico, que puede que incluso tengan en la clase, pero propongo otra vez recurrir a las TICs y optar por una opción on-line. Podemos encontrar distintas versiones en la red, como la siguiente: http://www.pequejuegos.com/juego-cuatro-en-raya.html

6. Pintando como Seurat

Para terminar, propongo trabajar con el punto de una forma totalmente

creativa. Ya les habremos enseñado algunas obras de arte realizadas con la técnica del puntillismo, como las de Seurat, y ahora deberán ser ellos los que se expresen libremente mediante la utilización de puntos. Para esta actividad es conveniente que trabajen con rotuladores de puntas de distintos grosores y con diferentes colores, sobre papel o cartulina, y haremos hincapié también en que relacionen esta técnica con la de los mosaicos. Como complemento, sería igualmente interesante que utilizaran alguna de las dos aplicaciones informáticas mencionadas para hacer esta tarea. En la imagen podéis ver un sencillo ejemplo que he realizado con Tux Paint.

Próximo capítulo:

Geometría para Primer Ciclo de Primaria - 2  El triángulo – Taller de MARTEMÁTICAS - 1

Taller de MARTEMÁTICAS - Introducción

Una de las claves del aprendizaje significativo está en la utilidad que tengan para los alumnos los conocimientos aprendidos; en la presencia que estos puedan tener en sus vidas cotidianas, tanto en la escuela como en su entorno familiar. De ahí la importancia que tiene la enseñanza globalizada en la escuela de hoy. Los niños aprenden así nuevos conceptos que ven que sirven para algo; los relacionan e identifican en distintas asignaturas simultáneamente, percibiendo su utilidad dentro y fuera del colegio.

Partiendo de esta idea, comienzo con esta entrada el primero de los talleres que voy a intentar ir desarrollando en este blog. El factor común de todos ellos será la Educación Artística, vinculada siempre con otras materias de Educación Primaria, como Matemáticas, Lengua Castellana y Literatura, Conocimiento del Medio o incluso Religión. La Historia del Arte nos lo pone fácil, pues no es difícil encontrar obras de arte clásicas y modernas relacionadas con las distintas disciplinas educativas, que nos puedan ayudar en nuestra labor.

No me voy a olvidar, por supuesto, de la Lengua Extranjera, en mi caso la lengua inglesa, que es la que conozco, pues como maestro de Inglés, de todos y cada uno de los talleres intentaré hacer su correspondiente versión en dicha lengua. Estos talleres en inglés resultarán especialmente útiles en los colegios bilingües, dentro o fuera del horario escolar, pues en ellos la tarea de motivar a los niños en el uso de la lengua inglesa de forma interdisciplinar no siempre resulta sencilla. Por último, como no sería ni lógico ni razonable predicar una cosa y hacer otra distinta, las TICs también jugarán un papel importante en el contenido y presentación de estos talleres.

Matemáticas y Arte

Dicho esto, voy a comenzar con las matemáticas. Relacionar Arte y Matemáticas puede parecer a simple vista algo artificial y forzado, pero nada más lejos de la realidad. Las matemáticas resultan fundamentales, de forma obvia en la arquitectura, pero también en la escultura y en muchas ocasiones en la pintura y otras artes, mal conocidas como “menores”, pero como no hay que olvidarse del pequeño público al que están destinados los talleres, me voy a centrar en la parte de las matemáticas cuya relación con el Arte y la expresión artística resulta más tangible y, por ello, más fácil de visualizar y entender por parte de los niños: la Geometría.

Así pues, esta primera serie, que he titulado: Taller de MARTEMÁTICAS, está dirigida inicialmente a alumnos del Primer Ciclo de Educación Primaria, trabajando las bases de la geometría, centrándonos en las formas planas: punto recta y plano, y dentro de estos últimos, en el triángulo, el círculo, el rectángulo y el cuadrado. Si el tiempo y las circunstancias me lo permiten, intentaré realizar entradas posteriores con pequeñas adaptaciones para adecuar el taller a  niveles superiores de Educación Primaria. Las obras de arte y referentes utilizados servirán, en líneas generales, para todos los ciclos, si bien la forma de presentarlas variará en función de la edad de los alumnos. Esta manera de presentación de contenidos será a veces diferente de como suelen aparecer en los libros de texto, aprovechando siempre para estimular la creatividad en los niños. Debo aclarar que no se trata en absoluto de sustituir a aquella enseñanza, más académica, sino de complementarla. De esta forma, los talleres servirán para afianzar unos conocimientos, para ayudar a comprenderlos si hay alguna duda, y para que resulte más motivadora su asimilación y, en el caso de su versión en inglés, servirán también de vehículo para familiarizar y motivar a los alumnos con un uso práctico y cotidiano de la lengua inglesa.

Presentación de los talleres

Los distintos talleres que vaya desarrollando, los iré presentando en este blog en forma de pequeños capítulos, mediante las correspondientes entradas del blog, pero debido a su extensión y complejidad, me limitaré en la mayor parte de ellos a introducir y presentar sus posibilidades educativas, sus contenidos y características más importantes. No obstante, y a modo de ejemplo, este primer taller sí que lo desarrollaré de forma completa, y en la última entrada del mismo, añadiré un enlace a una presentación interactiva del taller preparada para que cualquier maestro la pueda usar libremente en su clase.

Próximo capítulo:

Geometría para Primer Ciclo de Primaria - 1  El punto y la recta – Taller de MARTEMÁTICAS - 1.